Quiz sur les fractions

Correction de votre Quiz sur les fractions – Super !

Algèbre, Révision Brevet / Par

Cet article est la correction du quiz que je vous propose de faire sur cette page ci-dessous. Si vous n’avez pas encore testé votre niveau sur les fractions, je vous invite à cliquer sur le bouton ci-dessous pour faire le quiz :

Cliquez pour accédez au Quiz !

Ne vous inquiétez pas ! Nous vous proposerons de revenir sur cette page de correction à la fin du test de niveau. Vous pouvez donc cliquer sur ce bouton ci-dessus sans peur de perdre la page.

SOMMAIRE DE L'ARTICLE

Place à la correction !

Ne vous fiez pas à l’ordre des questions. Car lorsque vous faites le test, il génère les question et les propositions de réponses tout le temps dans un ordre différent. Ce qui permet de ne pas avoir toujours les questions dans le même ordre.

Question N°1 : Calculez 1/3 + 1

Etape 1 : Posons d’abord le calcul

\displaystyle \frac{1}{3}+1

Etape 2 : Remplaçons 1 par une fraction

On sait que : \displaystyle 1= \frac{1}{1}

Donc remplaçons 1 par \displaystyle \frac{1}{1} dans le calcul :

\displaystyle \frac{1}{3}+1=\frac{1}{3}+\frac{1}{1}

Etape 3 : Mettre toutes les frations au même dénominateur

Ici, le dénominateur communs à 1 et 3 est 3.

Donc multiplions \displaystyle \frac{1}{1} par 3, en haut et en bas :

\displaystyle \frac{1}{3}+\frac{1}{1}=\frac{1}{3}+\frac{1 \times 3}{1 \times 3}=\frac{1}{3}+\frac{3}{3}

Etape 4 : Simplifier le calcul en une seule fraction

Puisque nous avons les mêmes dénominateurs sur les deux fractions, alors nous pouvons mettre ces deux fractions sur un seul dénominateur :

\displaystyle \frac{1}{3}+\frac{3}{3}=\frac{1+3}{3}

Etape 5 : En déduire la solution

\displaystyle \frac{1+3}{3}=\frac{4}{3} \bigskip \\ \boxed{S=\{ \frac{4}{3} \} }

Question N°2 : a=5/4, b=3/2 et c=-5/2 Calculez l’expression a-bc

Etape 1 : On remplace les valeurs dans cette expression

\displaystyle a-bc= \frac{5}{4}-\frac{3}{2} \times (-\frac{5}{2})

Etape 2 : On calcul cette opération de fractions

La multiplication est prioritaire :

Donc on calcule en premier : \displaystyle -\frac{3}{2} \times (-\frac{5}{2})

On sait que la multiplication de deux nombres négatifs donne un résultat positif.
Ensuite, lorsqu’on multiplie deux fractions, on multiplie les numérateurs ensembles et les dénominateurs ensembles.

Donc ,

\displaystyle -\frac{3}{2} \times (-\frac{5}{2})=\frac{15}{4}

Maintenant l’addition :

L’expression complète ressemble maintenant à ça :

\displaystyle \frac{5}{4} + \frac{15}{4}

Les deux fractions sont au même dénomiteur. Donc, nous pouvons rassembler ces deux fractions sur un seul dénominateur :

\displaystyle \frac{5}{4} + \frac{15}{4} = \frac{5+15}{4}= \frac{20}{4}

Etape 3 : Fraction irréductible

La dernière opération est de la réduire pour la rendre irreductible :

\displaystyle \frac{20}{4}= \frac{5 \times 4}{4}= 5 \bigskip \\ \boxed{S=\{ 5 \} }

Question N°3 – Réduisez cette fraction en fraction irreductible : 28/42

Il y a plusieurs manière de réduire des fractions :

  • Soit un calule le PGCD(28;24), puis on simplifie en haut et en bas par le PGCD
  • Soit on recherche rapidement des facteurs communs à 28 et 42

Nous allons adopter la deuxième technique pour réduire cette 28/42. Si vous souhaitez connaître la manière de calculer un PGCD, je vous invite à consulter le cours gratuit sur la manière de Calculer un PGCD en utilisant la méthode originale du balayage :

Cliquez pour consulter le cours sur le PGCD

Etape 1 : Décomposer la fraction en facteurs communs

On sait que 28 = 4 x 7 et 42 = 6 x 7

On peut donc remplacer c’est valeurs dans la fraction :

\displaystyle \frac{28}{42}= \frac{4 \times 7}{6 \times 7}

Etape 2 : Réduire cette fraction

On peut barrer les 7 haut et en bas pour simplifier la fraction :

\displaystyle \frac{4 \times 7}{6 \times 7}=\frac{4}{6}

Etape 3 : Cette fraction est-elle irréductible ?

La fraction est irréductible seulement si on ne peut plus la simplifier.

Ici, on sait que 4 = 2 x 2 et 6 = 3 x 2

On peut donc simplifier à nouveau cette fraction :

\displaystyle \frac{4}{6}=\frac{2 \times 2}{3 \times 2}=\frac{2}{3} \bigskip \\ \boxed{S=\{ \frac{2}{3} \} }

Question N°4 – Calculez : 1/6+1/2+1/3 = ?

Etape 1 : Posons d’abord le calcul

\displaystyle \frac{1}{6}+\frac{1}{2}+\frac{1}{3}

Etape 2 : Mettre toutes les frations au même dénominateur

On sait que : 2 x 3 = 6

Donc le dénominateur communs sera 6.

Multiplions alors c’est diférentes fractions par le facteur adéquat pour obtenir un dénominateur de 6 partout :

\displaystyle \frac{1}{6}+\frac{1}{2}+\frac{1}{3}=\frac{1}{6}+\frac{1 \times 3}{2 \times 3}+\frac{1 \times 2}{3 \times 2}

On sait que : 2 x 3 = 6

Donc le dénominateur communs sera 6.

Multiplions alors c’est diférentes fractions par le facteur adéquat pour obtenir un dénominateur de 6 partout :

\displaystyle \frac{1}{6}+\frac{1 \times 3}{2 \times 3}+\frac{1 \times 2}{3 \times 2}=\frac{1}{6}+\frac{3}{6}+\frac{2}{6}

Etape 3 : Simplifier le calcul en une seule fraction

Puisque nous avons les mêmes dénominateurs sur les trois fractions, alors nous pouvons mettre ces trois fractions sur un seul dénominateur :

\displaystyle \frac{1}{6}+\frac{3}{6}+\frac{2}{6}= \frac{1+3+2}{6}

Etape 4 : En déduire la solution

\displaystyle \frac{1+3+2}{6}=\frac{6}{6} = 1 \bigskip \\ \boxed{S=\{ 1 \}}

Question N°5 – Observez ce calcul

\displaystyle \frac{72}{64}=\frac{9 \times 8}{8 \times 8} \bigskip \\

\displaystyle \frac{9}{8} est une fraction………….

A toi de trouver le mot manquant.

La fraction est-elle unitaire ?

Définition d’une fraction unitaire :

Une fraction unitaire est une fraction de la forme \displaystyle \frac{1}{n} , dans laquelle n est un nombre naturel non nul.

Exemples :

Des fractions comme  \displaystyle \frac{1}{2} ,  \displaystyle \frac{1}{3}  et  \displaystyle \frac{1}{10}  sont des fractions unitaires.

Résolution :

La fraction \displaystyle \frac{9}{8} n’est pas de la forme \displaystyle \frac{1}{n} . Donc \displaystyle \frac{9}{8} n’est pas une fraction unitaire.

La fraction est-elle périodique ?

Définition d’une fraction périodique :

Série dont les termes sont des fractions et dans laquelle le schéma des termes est répétitif.Si on exclut les cas où la période est une fraction nulle, une fraction périodique exprime un nombre rationnel qui n’est pas un nombre décimal.

Exemple

La fraction  \displaystyle \frac{2}{27}  est une fraction périodique puisque : \displaystyle \frac{2}{27}=\frac{74}{1000}+\frac{74}{1000000}+...... \bigskip \\

que l’on peut aussi écrire :   \displaystyle \frac{2}{27}=0,074074074..... .

Résolution :

\displaystyle \frac{9}{8}=1,125

On peut ne peut observer aucune périodicité dans ce résultats. Donc \displaystyle \frac{9}{8} n’est pas une fraction périodique.

La fraction est-elle équivalente ?

Définition de fractions équivalentes :

Des fractions équivalentes sont des fractions qui sont égales lorsqu’elles ont été réduites à leur plus simple expression.
Des fractions équivalentes représentent le même nombre rationnel.

Exemple :

Les fractions \displaystyle \frac{12}{18}  et  \displaystyle \frac{10}{15}  sont équivalentes, car elles sont toutes deux équivalentes au nombre rationnel  \displaystyle \frac{2}{3} .

Résolution :

On ne peut pas dire qu’une fraction est équivalente sans préciser à quoi elle est équivalente. Une fraction est équivalente à une autre fraction !

Donc cette proposition n’est pas correcte.

La fraction est-elle irréductible ?

Définition d’une fraction est irréductible :

Une fraction irréductible est une fraction dont le numérateur et le dénominateur n’ont pas de diviseur entier commun différent de 1. C’est une fraction qu’on ne peut plus réduire : elle est sous sa forme la plus simple.

Exemple :

  • Des fractions comme  \displaystyle \frac{2}{3} ,  \displaystyle \frac{3}{4} , sont des fractions irréductibles.
  • La fraction  \displaystyle \frac{8}{18}  n’est pas une fraction irréductible, car le nombre 2 est un diviseur entier commun à 8 et 18. Alors, la fraction irréductible équivalente à  \displaystyle \frac{8}{18}  est la fraction  \displaystyle \frac{4}{9}  qui est irréductible.

Résolution :

\displaystyle \frac{9}{8} est une fraction dont le numérateur et le dénominateur n’ont pas de diviseur entier commun sauf 1.

Donc \displaystyle \frac{9}{8} est une fraction irréductible.

Question N°6 – Cette fraction n’est pas simplifiable par ?

\displaystyle \frac{1278}{2130}

Pour être en mesure de répondre rapidement à cette question vous devais connaître les critères de divisibilité associé aux propositions contenues dans la question. Dans cette question, on nous demande par quoi n’est pas simplifiable \displaystyle \frac{1278}{2130} .

Par :

  • 2
  • 3
  • 5
  • 6

Etape 1 : Critères de divisibilité

2 : un entier est divisible par 2 (on dit aussi qu’il est pair) si son chiffre des unités est 0 ; 2 ; 4 ; 6 ou 8.

3 : un entier est divisible par 3 si la somme de ses chiffres est elle-même divisible par 3.

5 : un entier est divisible par 5 si le chiffre de ses unités est 0 ou 5.

6 : un entier est divisible par 6 s’il est divisible à la fois par 2 et par 3.

Etape 2 : Par quoi la fraction n’est pas simplifiable ?

Pour savoir si une fraction est simplifiable par un nombre, le numérateur et dénominateur doit être divisible, tous les deux, par ce nombre.

1278 et 2130 sont-ils divisibles par 2 ?

1278 et 2130 sont tous les deux des nombres paires.

Donc 1278 et 2130 sont divisibles par 2

1278 et 2130 sont-ils divisibles par 3 ?

Pour savoir si 1278 et 2130 sont divisible par 3, nous allons additionner tous les chiffres qui les composent :

1 + 2 + 7 + 8 = 18

18 est divisible par 3 : Donc 1278 est divisibles par 3.

2 + 1 + 3 + 0 = 6

6 est divisible par 3 : Donc 2130 est divisibles par 3.

Donc 1278 et 2130 sont divisibles par 3

1278 et 2130 sont-ils divisibles par 5 ?

Pour savoir si 1278 et 2130 sont divisible par 3, nous devons regarder le chiffre des unités :

Pour 1278, le chiffre des unités est 8.

8 ≠ 5 ou 5

Donc 1278 n’est pas divisibles par 5.

Le chiffre des untiés de 2130 est 0.

Donc 2130 est divisibles par 5.

Même si 2130 est divisible par 5, comme 1278 n’est pas divisible par 5, on peut donc conclure que la fraction n’est pas simplifiable par 5

Question N°7 – On considère la fraction suivante que l’on veut simplifier.

\displaystyle \frac{18}{81}

Une seule de ces affirmations est fausse, laquelle ?

  • On peut simplifier cette fraction par 3
  • Pour la rendre irréductible, il faut la simplifier par le PGCD(18;81)
  • On peut simplifier cette fraction par 9
  • Cette fraction est irréductible

Cette fraction est-elle simplifiable par 3 ?

Pour savoir si elle est simplifiable par 3, nous allons chercher si 18 et 81 sont divisible par 3 :

1+8 =9

9 est divisible par 3.

Donc 18 et 81 sont divisibles par 3

Pour la rendre irréductible, faut-il la simplifier par le PGCD(18;81) ?

Souvenez-vous que nous devons trouver un diviseur commun entre le numérateur et le dénominateur pour simplifier cette fraction. Le PGCD est le plus grand d’entre eux !

Donc si nous simplifions cette \displaystyle \frac{18}{81} par le plus grand des diviseurs communs à 18 et à 81, nous pourrons la réduire au maximum et la rendre irréductible.

Donc pour la rendre irréductible, nous pouvons la simplifier par le PGCD(18;81).

Est-elle simplifiable par 9 ?

Pour savoir si cette fraction est simplifiable par 9, nous devons chercher si 18 et 81 sont divisible par 9 :

1+8 =9

9 est divisible par 9, car un nombre est toujours divisible par lui-même.

Donc 18 et 81 sont divisibles par 9

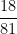\displaystyle \frac{18}{81} est-elle irréductible ?

Nous avons vu précédemment que \displaystyle \frac{18}{81} est simplifiable par 3 et par 9. Si \displaystyle \frac{18}{81} est encore simplifiable, c’est qu’elle n’est pas irréductible.

Question N°8 – Observez cette succession d’égalités :

\displaystyle \frac{2443}{1745} = \frac{7 \times 349}{5 \times 349} = \frac{?}{5}

Complétez le numérateur où se trouve le point d’interrogation.

Résolution

On sait que :

  • 7 x 349 = 2443
  • 5 x 349 = 1745

Ce qui signifie que 349 est un diviseur communs à 2443 et à 1745.

Si nous simplifions \displaystyle \frac{2443}{1745} par 349, nous trouvons \displaystyle \frac{7}{5} .

Donc le point d’interrogation correspond au chiffre 7.

Question N°9 : Trouvez la fraction correspondant à la partie colorée

Fraction en dessin

Résolution

Nous pouvons observer 4 cases colorées sur 20 cases au total.

Donc la fraction correspondant à la partie colorée est \displaystyle \frac{4}{20} .

Question N°10 : Trouvez la valeur de X

\displaystyle \frac{1}{2} = \frac{X}{8}

Résolution

C’est une équation du premier degré à une inconnue. Il suffit simplement d’effectuer un produit en croix pour trouver X.

\displaystyle X = \frac{1 \times 8}{2}= \frac{8}{2}=4 \bigskip \\ \boxed{S=\{ 4 \}} [/latex]

La préparation au Brevet, Stressant et long ! Pour plus de rapidité dans vos révisions, Révisez avec les différents « Packs de révision » qui vont vous permettre de vous perfectionner à l’épreuve de Mathématiques du Diplôme du Brevet :

Cliquez pour découvrir les “Packs de révision”

Vous pouvez vous spécialiser encore plus dans chacun des domaines qui sont :

L’Algèbre

Venez découvrir le “Pack Algèbre”

L’Arithmétique

Venez découvrir le “Pack Arithmétique“

La Maitrise des tableurs Excel

Découvrez le “Pack Fonctions et Gestion de données“

Les différentes vidéos contenues en ligne vous permettent de réviser quand vous le souhaitez, à vie et partout dans le monde du moment que vous disposez d’une connexion internet.

Articles actuellement consultés par des visiteurs

%d blogueurs aiment cette page :