Réviser l'épreuve de mathématiques du Brevet 2020 correction

Correction du QCM Épreuve de maths du Brevet 2020

Révision Brevet / Par

Voici comme promis la correction du QCM qui vous servira à réviser l’épreuve de Mathématiques du Brevet.

C’est parti ! Soyez attentif pour cette correction!

SOMMAIRE DE L'ARTICLE

Correction !

Question 1 : Résolvez 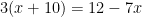3(x + 10) = 12 - 7x.

Correction :

\quad 3(x + 10) = 12\ - \; 7x

\Leftrightarrow 3x\; +\ 30 = 12\ -\; 7x \ Utilisez la distributivité !

\Leftrightarrow 3x\; +\; 30\; -\; 30= 12\; -\; 7x\; -\; 30\; On soustrait 30 de chaque côté de l’éqaution

\Leftrightarrow 3x = 12\; -\; 30\; -\; 7x\; On simplifie

\Leftrightarrow 3x = -18\; -\; 7x\; On simplifie à nouveau

\Leftrightarrow 3x\; +\; 7x = -18\; -\; 7x\; +\; 7x\; On ajout 7x de chaque côté de l’équation

\Leftrightarrow 3x\; +\; 7x = -18\; On simplifie

\Leftrightarrow 10x = -18\; On simplifie à nouveau

\Leftrightarrow \frac {10x} {10} = - \frac {18} {10} \; On divise par 10 de chaque côté de l’équation

\Leftrightarrow x = - \frac {18} {10} \; On simplifie

\Leftrightarrow x = - \frac {9} {5} \; On simplifie la fraction

Question 2 : Résoudre le système d’équations suivant :

\begin{cases}4x-3y=28 \\ y+6x=9 \end{cases}

Correction :

Etape 1 : On écrit y en fonction de x dans l’équation la plus simple.

\begin{cases}4x-3y=28 \\ y=9-6x \end{cases}

Etape 2 : On remplace l’expression de y précédemment trouvée dans l’autre équation.

\begin{cases}4x-3(9-6x)=28 \\ y=9-6x \end{cases}

Etape 3 : On simplifie l’équation qui ne contient qu’une seule inconnue.

On développe et on simplifie :

\begin{cases}4x-27+18x=28 \\ y=9-6x \end{cases} \Leftrightarrow \begin{cases}22x-27=28 \\ y=9-6x \end{cases}

Etape 4 : On résout l’équation qui ne contient qu’une seule inconnue.

\quad \Leftrightarrow \begin{cases}22x- \cancel{27}+\cancel{27}= 28+27\\ y= 9-6x \end{cases} \quad \Leftrightarrow \begin{cases}22x= 28+27\\ y= 9-6x \end{cases} \Leftrightarrow \begin{cases}22x= 55\\ y= 9-6x \end{cases} \Leftrightarrow \begin{cases}x= \frac {55} {22} = \frac {5} {2}\\ y= 9-6x \end{cases}

Etape 5 : On remplace la valeur de x dans la deuxième équation.

\; \Leftrightarrow \begin{cases}x = \frac {5} {2}\\ y= 9-6 \times \frac {5} {2} \end{cases} ~\Leftrightarrow \begin{cases}x = \frac {5} {2}\\ y= 9- \frac {30} {2} \end{cases} \; \Leftrightarrow \begin{cases}x = \frac {5} {2}\\ y= -6 \end{cases}

Question 3 : Combien de minutes y a-t-il en 3,5 heures ?

Correction :

3,5 h = 3h {\color{red} \times 60} + 0.5h {\color{red} \times 60} 3,5 h = 180 min + 30 min = 210 min

Question 4 : Calculer en valeur approchée \frac{1}{4}+0.5

Correction :

\frac{1}{4}+0,5 = 0,25+0,5 = 0,75

Question 5 : Laquelle de ces formes a le plus de côtés ? Encerclez votre réponse.

Correction :

  1. l’Hexagone possède 6 côtés
  2. l’Octogone possède 8 côtés
  3. le Parallélogramme possède 4 côtés
  4. le Trapèze possède 4 côtés

C’est donc l’Octogone qui possède le plus de côtés.

Question 6 : On considère la fonction g : x \longrightarrow x^2+7

Quelle formule doit-on entrer dans la cellule B2 pour calculer g(-2) ?

Fénêtre Excel. Question 6 du QCM pour réviser l'Épreuve de mathématiques du Brevet

Correction :

= A2^2 + 7

Question 7 : Si on développe et réduit l’expression (x+2)(3x-1)

Correction :

Etape 1 :On développe l’expression à l’aide d’une double distributivité :

(x+2)(3x-1) \; =3x \times x-1 \times x+2 \times 3x-1 \times 2 \\ \quad = 3x^2-x+6x-2 \\ = 3x^2 \; + \: 5x \;- \:2

Question 8 : L’hôtel de luxe

L’équipe de France de Football part en vacances dans un hôtel. Ils sont au total 25 personnes (joueurs + entraîneurs). Chaque personne prend une chambre individuelle. Ils ont décidé de dormir 6 nuits dans l’hôtel.

Une fois les vacances finies, l’hôtel leur donne une facture de 211 800 €. Dans cette facture, l’hôtel a insérer une taxe de séjour d’un total de 150 €.

Combien coûte le prix d’une seule chambre ?

Correction :

Etape 1 : On pose l’inconnue

Soit x le prix d’une seule chambre.

Etape 2 : On met en équation le problème

Prix total du séjour : 25x \times 6 +150

On a donc l’égalité suivante :

25x \times 6 + 150 = 211800

Etape 3 : On résout l’équation

\quad \quad \quad \Leftrightarrow 150x +150 = 211800 \\ \quad \quad \quad \Leftrightarrow 150x = 211800 - 150 \\ \Leftrightarrow 150x = 211650 \\ \Leftrightarrow x = \frac {211650} {150} \\ \Leftrightarrow x = 1411

Le prix d’une seule chambre coûte 1 411 € la nuit.

Question 9 : Écrivez le nombre six millions cinq mille deux cents en écriture scientifique.

Correction :

Etape 1 : Ecrivons d’abord ce nombre sous forme décimale.

6 005 200

Etape 2 : Déplaçons la virgule de 6 positions.

6&005&200,0 = 6,005&2000 \times 10^6 = 6,0052 \times 10^6

Question 10 : Inscrivez 36 comme produit des facteurs premiers.

Correction :

1; 2; 3; 4; 6; 9; 12; 18; 36

Si vous souhaitez connaître la méthode permmettant de trouver tous les diviseurs d’un nombre, lisez cette courte leçon :

Cliquez ici pour calculer tous les diviseurs de 36

Question 11 : Quelle est l’unité la plus appropriée pour mesurer la longueur d’un court de tennis ?

Correction :

Un court de tennis mesure plus d’un mètre de long et moins d’un kilomètre.

Mais comme la longueur d’un court de tennis est plus proche du mètre que du kilomètre.

Donc l’unité de mesure la plus appropriée est le mètre.

Question 12 : Calculer le PGCD de 135 et de 210.

Correction :

PGCD(135;210) = 15

Si vous avez un trou de mémoire, n’hésitez pas à consulter le cours sur la manière de Calculer un PGCD en utilisant la méthode du balayage :

Cliquez pour consulter le cours sur le PGCD

Question 13 : Calculer les solutions de l’équation suivante :

(3x+2)(3x-1)=0

Correction :

Un produit est nul si est seulement si au moins un de ses facteurs est nul.

Pour que cette équation soit égale à zéro, il faut :

  • soit que (3x+2) soit égale à zéro,
  • soit que (3x-2) soit égale à zéro.

On a alors la relation mathématique suivante :

\quad \quad 3x+2=0 \quad et \quad 3x-1=0 \\ \Leftrightarrow 3x=-2 \quad et \quad 3x=1 \\ \Leftrightarrow x_1= - \frac {2} {3} \quad et \quad x_2 = \frac {1} {3}

L’équation a deux solutions : \displaystyle -\frac {2} {3} et \displaystyle \frac {1} {3}

Question 14 : Voici une liste de numéros.

Trouvez la médiane.

21 17 23 21 29 32 21 25 36

Correction :

Etape 1 : Nous devons ranger cette liste dans l’ordre croissant.

17 21 21 21 23 25 29 32 36

Etape 2 : Déterminons la médiane.

La médiane est la valeur qui partage la population en deux sous-populations de même effectif.

On voit que 23 est au milieu de la liste.

Donc, la médiane est 23 car :

  • 4 nombres sint inférieurs à 23
  • et 4 nombres lui sont supérieur.

Question 15 : L’âge moyen des enseignants d’une école est de 36 ans. L’âge de Monsieur Calculis est de 11/9e de la moyenne.

Quel est l’âge de M. Calculis ?

Correction :

Monsieur Calculis à \frac {11} {9} de 36 ans :

Age_{Calculis}=\frac {11} {9} \times 36 = \frac {11 \times 36} {9} = 44

Monsieur Calculis à 44 ans.

Question 16 : Résoudre 4x - 3 = 14

Correction :

\quad \quad \quad \; 4x - 3 = 14 \\ \quad \quad \quad \quad \quad \Leftrightarrow 4x-3 { \; \color{red} +3}=14 { \; \color{red} +3} \\ \quad \quad \Leftrightarrow 4x = 14 +3 \\ \Leftrightarrow 4x = 17 \\ \; \: \Leftrightarrow \frac {4x} {4} = \frac {17} {4} \\ \; \; \Leftrightarrow \frac {\bcancel{4}x} {\bcancel{4}} = \frac {17} {4} \\ \Leftrightarrow x = \frac {17} {4}

Question 17 : La section d’un cylindre de révolution de diamètre 4 cm et de hauteur 10 cm par un plan parallèle à son axe, peut être :

Correction :

Cylindre avec une section parallèle à son axe.

Si la section est parallèle à l’axe du cylindre alors la longueur du rectangle est obligatoirement égale à la hauteur du cylindre.

On cherche donc dans les propositions une réponse avec une longueur de 10 cm.

Par conte, si la section n’est pas sur l’axe du cylindre, la largeur du rectangle sera inférieure au diamètre du cylindre.

La section est alors un rectangle de dimensions 3 cm et 10 cm.

Question 18 : Si une voiture roule à une allure régulière de 90 km/h. Quelle distance va-t-elle parcourir en 1 min ?

Correction :

La voiture roule à 90 km/h donc parcours 90 km en une heure :

[/latex] Vitesse_{Voiture} = 90 \; km/h = \frac {90 000 \; m} {1 \: h} = \frac {90000 \; m} {60 \: min} \\ \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \; = \frac {90000} {60} \: \frac {m} {min} = \frac {90000} {60} \: m/min \\ \quad \quad \quad \ = 1500 \; m/min [/latex]

Donc, la voiture va parcourir 1 500 mètres en 1 minute.

Question 19 : Manipulez cette équation pour trouver x.

y = \frac{x}{3} + 9

Correction :

\quad \quad \quad \; y = \frac{x}{3} + 9 \\ \quad \quad \quad \quad \Leftrightarrow y = \frac{x}{3} + \frac{9 { \; \color{red} \times 3}}{{ \; \color{red} 3}} \\ \ \ \ \ \quad \quad \Leftrightarrow y = \frac{x}{3} + \frac{27}{3} \\ \ \ \ \quad \quad \Leftrightarrow y = \frac{x+27}{3} \\ \ \ \quad \quad \quad \quad \quad \Leftrightarrow y { \ \color{red} \times 3} = \frac{x+27}{3}{ \ \color{red} \times 3} \\ \ \ \ \ \quad \quad \quad \quad \quad \Leftrightarrow y \times 3 = \frac{x+27} {\bcancel{3}} \times \bcancel{3} \\ \ \ \ \quad \quad \Leftrightarrow 3y = x+27 \\ \ \ \ \quad \quad \quad \quad \quad \quad \ \Leftrightarrow 3y { \ \color{red} - \ 27} = x+27 { \ \color{red} - \ 27} \\ \ \ \ \ \ \ \quad \Leftrightarrow 3y - 27 = x \\ \ \ \ \ \ \quad \Leftrightarrow x = 3y - 27

Question 20 : Un magasin vend deux marques de batteries. La marque A alimente un jouet pendant 5 heures, et est vendue en paquets de 8 pour 3,60 €. La batterie de la marque B alimente le même jouet pendant 5 heures et demie et se vend en paquets de 6 pour 2,94 €. Quelle est la marque la plus avantageuse ?

Correction :

Etape 1 : Calculons combien coûte une seule batterie :

Marque A :

Batterie_A = \frac {3,60 \ €} {8} = 0,45 \ €

Marque B :

Batterie_B = \frac {2,94 \ €} {6} = 0,49 \ €

Etape 2 : Calculons combien coûte une batterie pour une heure d’alimentation :

Marque A : On sait qu’une batterie coûte 0,45 € pour 5h d’alimentation.

Batterie_A = \frac {0,45 \ €} {5} = 0,09 \ €

Marque B : On sait qu’une batterie coûte 0,49 € pour 5,5h d’alimentation.

Batterie_B = \frac {0,49 \ €} {5,5} = 0,089 \ €

Etape 3 : Conclusion

Une batterie de la marque B coûte 0,089 € pour 1h d’alimentation.

C’est la marque la moins chère donc la marque B est la plus avantageuse.

Si vous avez encore de nombreuses peurs de rater votre Brevet, vous pouvez toujours accéder aux différents « Packs de révision » qui vont vous permettre de vous perfectionner à l’épreuve de Mathématiques du Brevet :

Cliquez pour découvrir les “Packs de révision”

Vous pouvez vous spécialiser encore plus dans chacun des domaines qui sont :

L’Algèbre

Venez découvrir le “Pack Algèbre”

L’Arithmétique

Venez découvrir le “Pack Arithmétique“

La Maitrise des tableurs Excel

Découvrez le “Pack Fonctions et Gestion de données“

Les différentes vidéos contenues en ligne vous permettent de réviser quand vous le souhaitez à vie et partout dans le monde du moment que vous disposez d’une connexion internet.

Articles récents

%d blogueurs aiment cette page :